Telegrafní klíč
Princip kvadraturního modulátoru
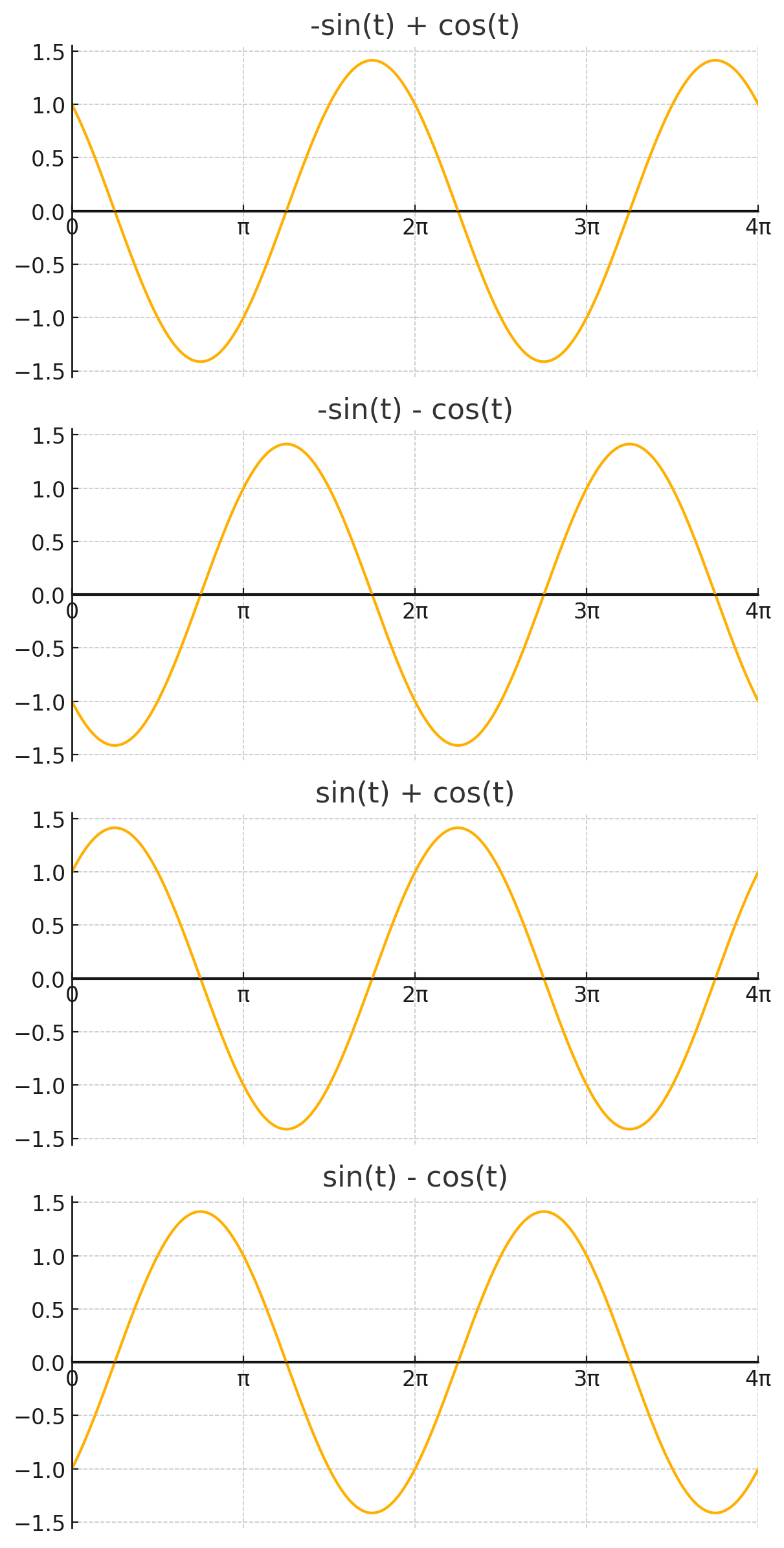
Kvadraturní modulátor pracuje na principu sčítání napětí s průběhem sinus a kosinus.
Níže je uveden matematický důkaz, že sčítáním funkce sinus a kosinus vznikne opět funkce sinus s jinou amplitudou a fázovým posunem.
Chceme sečíst sinusový a kosinusový průběhy se stejným kmitočtem: \$sin alpha + cos alpha\$
Nejprve funci kosinus nahradíme funkcí sinus podle vzorce: \$cos x = sin (x + pi/2)\$:
\$sin alpha + cos alpha = sin alpha + sin (alpha + pi/2)\$
Dále využijeme vzorec pro součet funkcí sinus: \$sin x + sin y = 2 cdot sin ((x + y)/2) cdot cos ((x - y)/2)\$
kde: \$x = alpha\$ a \$y = alpha + pi/2\$
\$sin alpha + cos alpha = sin alpha + sin (alpha + pi/2) = 2 cdot sin ((alpha + (alpha + pi/2))/2) cdot cos ((alpha - (alpha + pi/2))/2)\$
Výraz zjednodušíme:
\$2 cdot sin ((2 alpha + pi/2)/2) cdot cos ((-pi/2)/2) = 2 cdot sin (alpha + pi/4) cdot cos (-pi/4)\$
Protože: \$cos (-pi/4) = sqrt(2)/2\$:
\$2 cdot sin (alpha + pi/4) cdot sqrt(2)/2 = sqrt(2) cdot sin (alpha + pi/4)\$
Součtem funkcí sinus a kosinus se stejným kmitočtem vznikne funkce sinus s amplitudou \$sqrt(2) ~~ 1,41\$ a fází \$pi/4 tj. 45°\$.
Podobně bychom mohli postupovat pro jiné kvadranty.
QPSK